Lecture Notes, Chapter 1 & 5: Chemistry and Measurement

 

I.              Science

a.    What is science? Study of nature.

II.            Scientific method: series of steps used to explain a scientific question based on observations and experiments

a.    Observations: events or things that you happen to notice

b.    Example of an observation: Humans appear to die as they approach the age of 100.

c.    Hypothesis: an initial explanation (that can be tested) for observations

d.    Example of a hypothesis: People die because of their bad diets; improved diets will allow people to live forever.

e.    Experiment: a test of the hypothesis. Rejects or accepts hypothesis

f.     Theory: the best explanation for the observations, based on the results of many experiments

g.    Law: a generalized summary of observed behavior

h.    Law: what always happens. Theory: explanation for what always happens.

i.      Example of a law: “All living things eventually die.” Example of a theory: “All people die because of  a combination of their diets and because of genes in their DNA that tells their body that it is time to die.” (Note: I have no idea if that theory is actually true!)

j.      Without the scientific method, science becomes philosophy or just a big waste of time.  Biggest problem of fake science: untestable or lack of hypothesis.

                                          i.    Ex: prove that we haven’t been in class for a million years

                                        ii.    Ex: the earth stays near the sun because it likes the sun

 

III.           Chemistry

a.    What is chemistry? The study of matter and the changes it undergoes.

                                          i.    Biology: living things

                                        ii.    Physics: forces and how they affect matter

                                       iii.    All sciences overlap: biochemistry, physical chemistry, cosmochemistry, psychopharmacology, etc.

b.    Origin of chemistry: alchemy.

                                          i.    Alchemy (from Merriam-Webster): the medieval chemical science and speculative philosophy whose aims were the transmutation of the base metals into gold, the discovery of a universal cure for diseases, and the discovery of a means of indefinitely prolonging life

                                        ii.    Alchemists were not scientists. More like religious philosophers who cooked chemicals. Discovered some useful “recipes”: how to prepare certain acids, how to isolate and purify certain elements.

                                       iii.    Alchemists: never found a way to turn a common metal such as iron or lead into gold.

c.    Modern chemistry: began with the use of careful measurements and experiments. Father of modern chemistry is Antoine Lavoisier, who was murdered (guillotine – at least it was fast) during the French Revolution. The mobs of citizens were mad about the king, so of course they killed Lavoisier (a former tax official). Another scientist dies at the hands of the masses. Please don’t do this to Mr. Mac if you are mad about your grades.

IV.          Safety demonstration: coffee creamer + match + air

V.           Demonstration: Volume, and Perception and Volume  - pouring colored water between grad cyl, metric cube, beaker

a.    Graduated cylinders are for measuring, beakers are for mixing.

VI.          Scientific notation – why use it? Sci not used to express very large and very small numbers. Awkward to write such numbers without using powers of 10

a.    Example: Avogadro’s number, which is the number of atoms in a gram of the lightest element, hydrogen. 6.02 x 1023 =602,000,000,000,000,000,000,000

b.    Example: the mass of an atom of hydrogen: 1.66 x 10-24g = 0.00000000000000000000000166 g

c.    Sci not = must be expressed as a power of 10, must have only one number to the left of the decimal

d.    Convert the following numbers to sci not:

                                          i.    5403

                                        ii.    0.000321

                                       iii.    20

                                       iv.    2

                                        v.    548.4 x 105

                                       vi.    0.000562 x 106

                                      vii.    0.000562 x 10-3

e.    How to enter scientific notation into your calculator

f.     How to set menu of your graphing calculator to scientific notation – do not limit number of decimal places!

VII.         Units: they tell you the scale or standard of a measurement

a.    SI = International System is the system of units that we use in chemistry class, and what is used in all scientific work. “international language of measurement”

b.    Metric Prefixes:

                                          i.    Make base units bigger or smaller

                                        ii.    See table 2.2, p. 19

                                       iii.    Memorize centi (c), milli (m), kilo (k)

 

 

Type of measurement

Abbreviation

Definition

Units

Instrument

length

l

dist between two points

m

meters

ruler

area

A

= l x w

m2

square meters

ruler

volume

V

Amount of space that something occupies

= l x w x h

m3

cubic meters

also ml, cm3, cc; l and dm3

ruler or graduated cylinder

*meniscus

mass

m

Amount of mater in an object

kg

kilograms

also g

balance

weight

F or W

The force due to the pull of  gravity on an object

N

newtons

scale

density

D

=m/V

g/cm3

g/ml

grad cyl + balance

temperature

T

Average kinetic energy of the particles in a substance

degrees Celsius (C) or Kelvins (K)

thermometer

heat

Q

The total amount of energy in an object due the motion of its atoms

joules (J) or calories (cal)

calorimeter

time

t

(disregard)

s

seconds

clock, watch

 

VIII.       Measurement: how to make measurements with a ruler, grad cylinder, and a balance



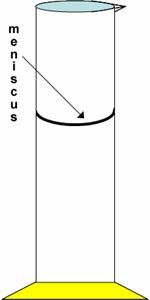
a.    Major point: figure out how many decimal places that the instrument can supply, and then estimate one more place – no more and no fewer – when recording the measurement (fig 2.5, p.24)

b.    Ruler: typically marked to the nearest mm, so read to the nearest 0.1 mm

c.    Grad cyl: marked to the nearest ml, so you should read it to the nearest ___? (nearest 0.1 ml)

d.    Buret: marked to the nearest 0.1 ml, so you should read it to the nearest ___? (nearest 0.01 ml)

e.    Triple beam balance typically is marked off to the nearest 0.01 g, thus you must estimate one more place and record mass to the nearest _____? (nearest 0.001 g)

f.     How should we record volume of 10 ml cyl? 1000 ml cyl?

g.    Don’t forget to always read the bottom of the curved surface of the liquid in a graduated cylinder, which is called the meniscus.

                                          i.    Meniscus formed due to hydrophilic nature of glass. What does hydrophilic mean?  (“water loving”) Hydrophobic? (water-fearing) Ex of hydrophobic: wax paper. This stuff won’t be on a quiz (yet).

h.    Tricky: what if the level of water in 100 ml grad cyl (with 1-ml markings) is right at the 70-ml mark? Can we just record the volume as 70 ml? No. Must still record to the nearest 0.1 ml. Thus, 70.0 ml.

IX.          Significant figures

a.    Significant figures are all of the numbers in a measurement that are recorded plus one more digit that is estimated. Forget the definition, learn the concept. J

b.    Imagine a piece of string that is 1 meter long. You measure it with a basic, primitive meter stick, so you know it is 1 meter long.

                                          i.    Now divide it up into three equally-sized pieces by folding the string and cutting it

                                        ii.    How long is each piece? 13 = 0.333333333333 etc meters long

                                       iii.    Does this really make sense? The original string was measured with a fairly primitive instrument, but now the pieces that came from that original string are known to the trillionth (or even less) of a meter?!?!  Dude – that’s smaller than the radius of an atom!

c.    Important: In science, the meaning of the measurement is as important as the recorded value (size).

                                          i.    Do the measurements “10 m” and “10.000 m” mean the same thing, even though they are the same size?

d.    Furthermore, all numbers are not measurements

e.    Math = deal with numbers. Science = deal with measurements. The above calculation (using numbers only) would be correct in math class, but when measurement is involved (numbers + units), this becomes a science question. Therefore, the answer must be rounded. (The correct answer is 0.3m – we’ll explain why later.)

f.     All measurements have some uncertainty. A very sensitive  instrument can be used to make measurements in very small increments. Such an instrument will have little uncertainty, but it will still have some uncertainty!

g.    A measurement that is known with great certainty has a lot of significant figures. A measurement that is not known with great certainty has few significant figures. A measurement that is not known with great certainty is an approximate measurement. All measurements – even measurements made with the best instruments in the world – are approximate to some extent.

h.    How many significant figures are there in a measurement made when 100 ml of water is measured in a grad cylinder?

                                          i.    With 10 ml markings? (3)

                                        ii.    With 1 ml markings? (4)

                                       iii.    With 0.1 ml markings? (5)

i.      Determining the # of sig figs – see page 25-26.

j.      How about expressing “100 ml” to the following number of sig figs?

                                          i.    1 sig fig

                                        ii.    2 sig figs

                                       iii.    3 sig figs

                                       iv.    4 sig figs

                                        v.    5 sig figs

                                       vi.    Do Ex 2.2, p. 25

k.    Rounding off numbers – a review! J

X.           Rules for sig figs in calculations

a.    Multiplication/division rule: consider all of the sig figs in the measurements involved in the calculation. The answer can have no more sig figs than the measurement with the least number of sig figs.

b.    Addition/subtraction rule: consider only the sig figs to the right of the decimal point in the measurements involved in the calculation. The answer can have no more sig figs to the right of the decimal point than the measurement with the least number of sig figs to the right of the decimal point.

c.    Ex. 2.4 & 2.5, p. 27

d.    Thus, the answer to the string problem above:

 

1 m 3 = 0.3333 . . . = 0.3 m (original measurement had only 1 sig fig)

 

XI.          Accuracy & Precision

a.    Accuracy: how close a measurement is to the accepted value

                                          i.    Perfect accuracy: the measurement (or average of several measurements) is exactly the same as the accepted value

                                        ii.    Our measure of accuracy  is % error

                                       iii.    Perfect accuracy = 0% error

 

b.    Precision: a measure of the repeatability of a measurement

c.    Perfect precision: every single measurement in a set of measurements is the exact same

                                          i.    Example: Imagine that you work at an ice cream store. At the end of your shift, have to count all of the money in your cash register drawer. If you count out the money three times and get the exact same amount of money each time, then your precision is excellent (perfect, in fact).

                                        ii.    However, if you happened to count the money incorrectly each time (maybe two twenty-dollar bills were stuck together, for example) you have poor accuracy . . . even though you have great precision!

d.    One measure of precision is average deviation

e.    Perfect precision is average deviation = 0

f.     The “Dart Board” analogy of accuracy and precision:



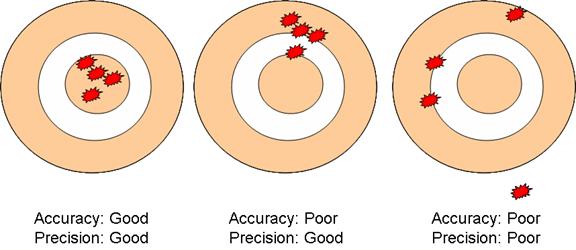
g.    Accuracy and precision are used to describe experimental data. Example problem: Given: the density of the metal aluminum is 2.70 g/cm3 (Table 2.8, p. 44). Thus, the accepted value for the density of aluminum is 2.70 g/cm3.  The experimental value is what the student experimenters determined to be the density.

 

Trial

miguel

Jermaine

Becky

1

2.69

4.2

3.72

2

2.72

2.08

3.64

3

2.72

3.44

3.72

4

2.63

1.00

3.69

AVERAGE

2.69

2.68

3.69

 

·         Miguel’s accuracy was _____ and his precision was ______.

·         Jermaine’s accuracy was _____ and his precision was ______.

·         Becky’s accuracy was _____ and her precision was ______.

 

XII.         Safety Lecture. Refer to handout. Sign safety contract. Have parents sign Safety Contract- turn it in tomorrow! J

XIII.       Dimensional analysis

a.    Dimensional analysis is a simple way to convert from one type of measurement units to another, hopefully mistake-free! The idea is that if you can “cancel” the units like fractions, you can get the write answer.

b.    Ex: 10 kg = _?_ g Sure, we know that we need to move the decimal place. You may even know that it needs to be moved 3 times.  But which way do we move it? (Answer = 10,000 g)

c.    First, let’s practice fractions:

                      

 

                       

 

d.    Now, units work the same way. Let’s start with a conversion that all of us can solve in our heads.

 

12 apples = _____ doz        24 apples = _____ doz       

 

30 apples = _____doz         4 doz = _______apples

 

e.    Next, let’s try to solve these same problems with dimensional analysis.

 

   

 

or, for the last problem

 

 

      

 

 

 

10 kg = _____g               10g = _____ kg         10.0 L = _____ mL

 

10 ml = _____ L              162.3 cm = ___m      162.3 km = _____m

 

These one-step problems (see above) will be the subject of your next quiz, “Dimensional Analysis I.”

f.     Now, two-step and multi-step problems:

 

2.00 hrs = _____ s          2.00 s = ____ hrs      35.0 days = _____ s

 

65.9 km = ____ cm         65.9 cm = _____ km

 

g.    Next, complex unit conversion

 

Problem:

 

Strategy: 

 

Solution:

 

 

Problem:  An animal is traveling at a rate of 3.5 cm/s. How many km/hr is this?

 

Problem: 

 

Strategy:

 

Solution:

 

h.    Cubic units conversion.

                                          i.    Finally, how can we convert cubic units? There are 10 cm in 1 dm, for instance, but there are not 10 cm3 in  1 dm3. Thus,

                                        ii.    Example: Convert 3.48 mm3 to m3. (Start by determining how many mm3 there are in 1 m3.)

 

XIV.      Temperature and Heat.

a.    Temperature is a measure of the average kinetic energy of the particles in a substance. This means that the faster the particles in a substance move, the higher its temperature. Temperature can also be thought of as “how hot or cold an object is.”

b.    Heat, on the other hand, is a form of energy that takes into account not only the energy of the particles, but the number of particles as well. It takes more heat to bring a pot of boiling water to a boil than it does to bring a cup of water to a boil. However, a pot of boiling water and a cup of boiling water have the same temperature.

c.    Temperature is measured in degrees Celsius (C) or in Kelvins (K).

 

 

Type of measurement

Abbreviation

Definition

Units

Instrument

temperature

T

Average kinetic energy of an object

degrees Celsius (C) or Kelvins (K)

thermometer

heat

Q

The total amount of energy in an object due the motion of its atoms

joules (J) or calories (cal)

calorimeter

 

d.    The Celsius scale is based on the freezing and boiling points of water. Water freezes at 0 C and boils at 100 C (under ordinary conditions). However, the lowest temperature possible is not 0 C.

                                          i.    The lowest temperature possible is -273.15 C, which is given the value zero on the Kelvin scale. This lowest temperature is the point at which the molecules in a substance would stop completely. This temperature is called absolute zero.

                                        ii.    To convert from C to K, use this formula:

K = C + 273           

                                       iii.    You can covert from K to C by using the same formula
(C = K -273).

                                       iv.    Most Americans are familiar with the Fahrenheit scale. We will not use this scale in class. (Few people -- scientific or otherwise -- outside of the U.S. use the Fahrenheit scale.)

 

 

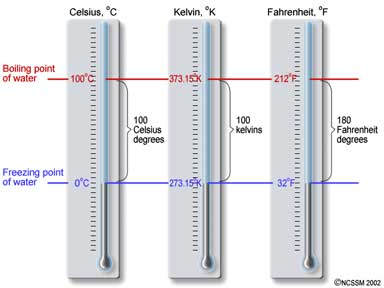
        Do ex. probs. 2.8 (p.35) and 2.9 (p. 37).

 

XV.        Calculating volume and density

a.    The volumes of rectangular solids (e.g., cubes) and cylinders are fairly easy to calculate:

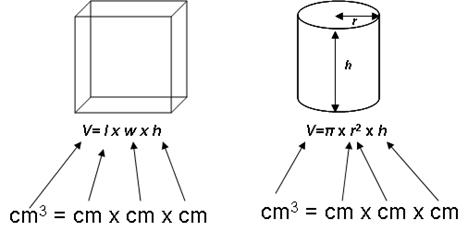
b.    However, the volumes of irregularly-shaped objects (or substances in powdered, liquid, or gaseous form) are difficult or impossible to measure this way. It is easier to measure volume in these cases by volume displacement.



c.    What is the volume (in ml) of the irregularly-shaped object above?

d.    Density is the mass per unit volume of a substance. It’s kind of like how “tightly packed” something is. (That’s not really an accurate statement, but it will do for now.)

                                          i.    Important: Density  mass. Density  heaviness. Density  weight.

                                        ii.    Example:

1.    Is steel heavier than water? Can’t answer this question! A nail, for instance, is lighter than a gallon of water. On the other hand, the engine of your car (mostly steel), is heavier than a gallon of water.

2.    However, if you throw ANY amount of steel into ANY amount of water, the steel will always sink.

3.    Steel is not necessarily heavier than water, but it is ALWAYS DENSER than water.

                                       iii.    Tricky: Are humans denser than water? (Hint: try walking across or lying across the surface of a bathtub of water!)

                                       iv.    Trickier: why do steel ships float? (Hint: what usually happens right before they sink?)

                                        v.    Extra Nerd Points: fill a glass with ice cubes, and then fill the glass to the rim with water. Let the ice melt. Bet someone $50 that the glass won’t overflow. (So much for the world going underwater when the polar icebergs melt!?!!)

e.    Calculating density
 

f.     Units of density, therefore, are typically g/cm3 (same as g/ml).

g.    I will give you this and all necessary formulas for the tests and quizzes this year unless otherwise stated.

h.    Practice problems:

                                          i.    Example 2.13, p. 44

                                        ii.    Example 2.14, p. 45

                                       iii.    Example 2.15, p. 46

i.      Don’t forget: 1 cm3, often abbreviated a “cc” (for cubic centimeter), is the exact same size as a milliliter (ml or mL)

                                          i.    1cm3 = 1ml = 1 cc  . . . always always always!

                                        ii.    1dm3 = 1 liter  . . .  always always always!

 

j.      Important point:

 

If something sinks, it is because that thing or substance is denser than the medium surrounding it. If something floats, it is because that thing or substance is LESS dense than the surrounding medium.

 

k.    Refer to Table 2.8, p. 44.

                                          i.    Will iron sink in water?

                                        ii.    Will iron sink in mercury?

                                       iii.    Will gold sink in mercury?

                                       iv.    If benzene, water, and ethanol are poured into the same beaker, which liquid will float to the top? Which will sink to the bottom? Which will be in the middle?

                                        v.    Notice that the densities of gases are much, much lower than the densities of liquids and solids.

l.      And finally, here is something that you MUST memorize: the density of water is 1.00 g/cm3. (D of H2O = 1.00 g/ml.)